بحث عن المتجهات في الفضاء الثلاثي الابعاد
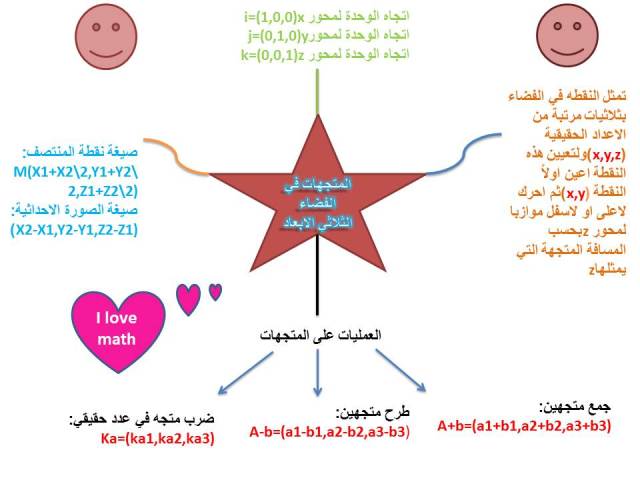 |
البحث عن المتجهات في الفضاء ثلاثي الأبعاد من البحث الذي يُطلب غالبًا من الطلاب في موضوعات الرياضيات والفيزياء ، حيث لا يمكن معرفة وفهم العديد من موضوعات الفيزياء إلا بعد فهم المتجهات والعمليات التي يمكن إجراؤها عليهم؛ من الضرب والطرح والجمع ، لأن الكميات في الفيزياء مقسمة إلى كميات متجهة وكميات غير متجهة ، أو تسمى كميات قياسية ، والكميات القياسية يسهل التعامل معها ونحن بالطبع معتادون عليها ، لكن العقدة هنا ينشأ في ضرورة تعلم الاتجاهات لفهم كميات المتجهات.
تعريف النواقل في الفضاء ثلاثي الأبعاد
يتم تعريف المتجه على أنه كمية ذات حجم واتجاه وهندسة. يمكننا أن نتخيل متجهًا على شكل قطعة مستقيمة موجهة ، يكون طوله هو مقدار المتجه ، وفي نهايته سهم يشير في الاتجاه ؛ حيث يكون اتجاه المتجه من ذيله إلى رأسه. يكون المتجهان متطابقين إذا كان لهما نفس الحجم والاتجاه ، فهذا يعني أنه إذا أخذنا متجهًا ونقلناه إلى موضع جديد بينما بقينا في نفس الاتجاه ، فإن المتجه الذي سنحصل عليه في نهاية هذه العملية هو نفس المتجه الذي كان لدينا في البداية. ومن أمثلة المتجهات نواقل القوة والسرعة ؛ كل من القوة والسرعة في اتجاه معين ويشير طول المتجه إلى حجم القوة أو مقدار السرعة. [1]
ابحث عن المتجهات في الفضاء ثلاثي الأبعاد
مقدمة عن البحث: الكميات المتجهة من الأمور التي يهتم بها الفيزيائيون بشكل كبير ، لأنه لا يمكن إجراء عمليات رياضية على الكميات الفيزيائية إلا من خلال فهم المتجهات ، ما هو مفهومها ، وكيف يمكننا التعامل معها ، وفي هذا البحث نقوم سيقدم لك شرحًا كاملاً عن النواقل
شرح المتجهات في الرياضيات
أول شيء يجب أن تتعلمه هو أن المتجه يُشار إليه بحرف إنجليزي وفوق سهم مثل هذا (→) ، بينما يُشار إلى الكمية القياسية فقط بحرف بدون سهم فوقه ، وفي الصورة التالية يمكنك ملاحظة أن المتجه الذي يرمز إليه بالحرف (أ) هو متجه موجود في بعدين اثنين ، وهنا سأبدأ بشرح لك عن المتجه في بعدين بسبب سهولة هذا الموضوع ، وهنا يمكن تحليل المتجه أ إلى مكونان من خلال عمل إسقاط رأسي على كل من محوري x و y للحصول على إسقاط رأسي وإسقاط أفقي ، ونشير إليهما على التوالي بالرمزين (AY ، AX) ؛ حتى نتمكن من كتابة المتجه بطريقتين ، الأولى بكتابة مكوناتها ، والثانية بكتابة المقدار والزاوية ، كما ذكرنا سابقًا.
ابحث عن المتجهات في الفضاء ثلاثي الأبعاد
من الهندسة السابقة ، نستنتج أن المتجه A يمكن كتابته على النحو التالي: (A = AY + AX). الطريقة الثانية هي كتابة التعبير متبوعًا بالزاوية على النحو التالي: (أ ∠θ). مع ملاحظة أننا أهملنا وضع السهم فوق الكميات المتجهة لأن هذا أمر صعب.
- تعريف المتجهات في الفضاء الثلاثي الأبعاد
- المتجهات في الفضاء الثلاثي الأبعاد pdf
- بحث عن المتجهات في الرياضيات
- بحث عن المتجهات في الفضاء الثلاثي الأبعاد doc
- حل المتجهات في الفضاء الثلاثي الأبعاد
- شرح المتجهات في الرياضيات
- كتب عن المتجهات
- خصائص المتجهات

